Tomas Härdin1
La defensa de la planificación
Estos últimos años la situación climática y la incapacidad de las economías de mercado para abordarla me ha llevado a leer teoría política e intentar entender qué se puede hacer. No he escrito mucho sobre este viaje aquí [en el blog], pero aquellos que me conocen saben que este proceso se lleva produciendo desde hace un buen rato. Mi conclusión por ahora es que los viejos cibernéticos soviéticos iban por el buen camino.
Todo esto está relacionado con lo que se conoce como Problema del Cálculo Económico (PCE). El debate gira en torno a si la planificación es factible como reemplazo a los mercados. Este debate se produjo principalmente en la época de entreguerras y no tiene una conclusión satisfactoria. Desde la disolución de la URSS entre 1989-1991, el debate parece haberse decantado en favor de los mercados. Tras la caída de la URSS, la idea del capitalismo de libre mercado como estadio final de la humanidad emergió, lo que conocemos hoy como neoliberalismo, la ideología global dominante.
Hoy en día, el neoliberalismo se enfrenta al reto de cómo abordar la presente catástrofe climática de una manera que no lastre de manera indebida a la élite no electa que posee la economía. Esto da lugar a políticas que crean tensión entre diferentes secciones de la clase trabajadora. Un ejemplo reciente de esto es el movimiento de los chalecos amarillos, provocado por las tasas al combustible del gobierno de Macron.
Una causa de la subida de movimientos como los chalecos amarillos es la idea de que las emisiones de gases de efecto invernadero (GHG) tienen que tener un coste. Y como todos sabemos, todo lo que tenga un coste fijo es efectivamente gratis si eres rico y las tasas al consumo, como el IVA, son regresivas en la práctica. Otra complicación es que a la gente que vive en las ciudades les afectan menos las tasas a los combustibles que a la gente de las áreas rurales, especialmente aquí, en el norte de Suecia, donde las distancias son grandes y la mayoría de servicios sociales se han movido a las ciudades.
La solución justa y racional a la situación climática, que el mercado ha sido incapaz de gestionar, es una economía global planificada. No me voy a preocupar demasiado con la política detrás de estos posts, si no es para decir que prefiero un proceso político lo más democrático posible. También debería señalarse el hecho de que los sitios de trabajo donde la mayoría de nosotros pasa la mitad de nuestro tiempo diurno no son de ninguna manera democráticos. En la mayoría de las empresas privadas, todas las decisiones las toman los propietarios, que nunca son elegidos o sacados por sorteo o ningún proceso de este tipo. Además, ninguna empresa usa un sistema de mercado interno. Tampoco lo hacen las familias.
Más allá de ser más democrática, la planificación también tiene el potencial de ser mucho más eficiente que los mercados, lo que significa que el mismo nivel de vida puede ser mantenido con menos input de trabajo. Esto será importante cuando la humanidad haga la transición del capitalismo a una economía de estado estacionario sostenible.
Por qué el problema del cálculo económico es más fácil de lo que se pensaba anteriormente
En los años 20 hasta los años 40, cuando el debate del PCE estaba en boga, el contraargumento a la planificación económica de gente como Friedrich Hayek era que simplemente no había una manera práctica de asignar racionalmente recursos in-natura para una economía entera. Si tienes 1000 bienes entonces necesitarías 1000^3 = mil millones de operaciones para resolver las ecuaciones lineares respectivas. Así que el argumento decía que un equipo de humanos trabajando con calculadoras no podría esperar terminar los cálculos en el tiempo de una vida humana, incluso para economías bastante modestas.
Para el lector moderno puede haber quizás una solución obvia al problema: los ordenadores (computadores). En la época en la que se producía el debate del PCE, la palabra computador era un trabajo, como profesor o fontanero. Pasaría un tiempo tras la segunda guerra mundial hasta que la ciencia de los ordenadores (informática) se pudiese establecer propiamente. Los ordenadores modernos pueden hacer miles de millones de cálculos por segundo, de manera barata.
¿Qué clase de computaciones necesitamos?
Una vez que ha quedado claro que los ordenadores pueden planificar la actividad económica, la pregunta pasó a ser “¿cuánto?”. ¡La respuesta resulta ser “mucho”!
Wassily Leontief desarrolló el concepto de análisis input-output hacia 1936. Esto involucra encontrar la solución de un sistema de ecuaciones lineales de la forma (I-A)x=d donde A es una matriz de coeficientes técnicos que dice cuánto de cada bien es necesario para producir una unidad de otro bien, d es un vector dado de las demandas finales y x el vector que dice cuántas unidades de cada bien producir, incluyendo bienes intermediarios. Resolviendo este sistema ingenuamente usando eliminación Gaussiana toma un tiempo cúbico del número de variables. Pero tal y como señaló Leontief, la matriz A tiene muchas entradas que son 0. A es dispersa.
Lidiar con matrices dispersas es en el presente un campo científico en sí mismo. Los ordenadores modernos resuelven sistemas lineales dispersos de decenas de millones de variables de manera rutinaria, y grupos de computadoras pueden lidiar con miles de millones de variables. Hasta aquí muy bien.
¿Cuál es el truco?
Resolver sistemas de ecuaciones lineales no es suficiente. En realidad, hay limitaciones a cuánto puede producir cada industria, cuánta gente puede trabajar en cada industria, limitaciones de transporte, cuántos gases de efecto invernadero se emiten etc… Resolver sistemas de ecuaciones condicionados como estos se llama programación lineal (PL). La PL es un problema mucho más difícil que simplemente resolver una ecuación lineal. Tanto es así que se supone que toma tiempo exponencial en el número de variables, no cúbico. ¡Mal asunto!
¿Cómo resolvemos la PL en un tiempo razonable?
La clave para usar la PL para la planificación económica es darse cuenta de que no necesitamos la solución óptima. Una solución aproximada funciona igual de bien, bajo supuesto que esté suficientemente cerca del óptimo, digamos a un 1%. Hay una clase entera de algoritmos que pueden hacer eso. La siguiente tabla es un resumen con notación simplificada gran-O:
| Quién | Cuándo | Complejidad | Peor caso |
| Khachiyan | 1979 | O(n6 L) | O(n6 L) |
| Karmarkar | 1984 | O(n3,5 L) | O(n3,5 L) |
| Renegar | 1988 | O(d2,373 n0,5 L) | O(n2,873 L) |
| Vaidya | 1989 | O((n+d)1,5 n L) | O(n2,5 L) |
| Lee y Sidford | 2015 | O((nnz(A)+n2) n0,5 L) | O(n2,5 L) |
| Cohen, Lee y Song | 2020 | O(n2,373 L) | O(n2,373 L) |
nnz(A) es el número de elementos no nulos en A, d es el número de variables, n es el número de restricciones, d < n. L es la precisión deseada para la solución, en bits.
En la práctica muchos de estos algoritmos son más lentos ya que la multiplicación de matrices es O(n^2,8) para un n que los ordenadores puedan manejar. Para una economía real n va a ser del orden de 10^9, lo cual sigue haciendo la computación impracticable si se hace en un solo ordenador. Hay una necesidad de evaluar cómo de bien pueden resolver PL grupos de ordenadores, especialmente cuando el número de nodos N se acerca a raíz(n), n o hasta nn(A). La noción aquí es que cada lugar de trabajo podría tener un ordenador que participase en el proceso de planificación, o un grupo de ordenadores por ciudad, todos conectados por internet. Cuantos más nodos se conectan juntos, más eficiente será la economía.
En un post posterior, entraré en detalle en mis investigaciones sobre qué algoritmos parecen adecuados para la paralelización y algunos resultados experimentales.
Otras consideraciones
Las ideas en esta sección están principalmente sacadas del artículo de 2020 de Spyridon Samothrakis.
Las economías reales no son lineales. Hay sinergias, gastos generales, depreciación y rendimientos decrecientes. El gráfico siguiente ilustra cómo los requerimientos (‘inputs required’) de una sección de la industria química pueden depender de cuanta producción se requiere (‘output requested’):
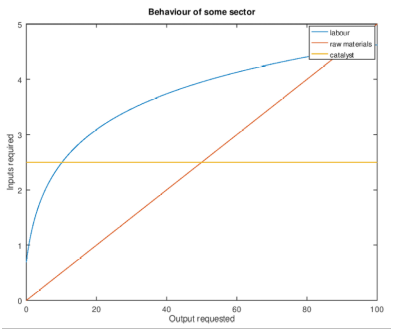
La línea para materias primas (‘raw materials’) demuestra el tipo de modelo lineal que Leontief asume. La curva de trabajo (‘labour’) demuestra cómo la producción a gran escala puede reducir los requerimientos de trabajo marginales en algún sector, y que la producción a pequeña escala resulta en un rendimiento mediocre. La curva de trabajo tampoco es nula para ninguna producción lo que modeliza el hecho de que algunas industrias tiene gastos generales fijos inherentes a la producción. Finalmente, la curva del catalista (‘catalyst’) sirve para demostrar que hay requerimientos que varían muy poco independientemente de la demanda.
Este tipo de comportamiento no lineal puede variar mucho entre sectores distintos. En principio puede ser capturado por linearización por partes. Otra opción es ir hacia programación cuadrática (QP) o programación matemática general.
Lecturas más allá2
Para una visión de conjunto de cómo una sociedad basada en torno a la planificación por ordenadores puede funcionar, recomiendo leer Towards a New Socialism de Paul Cockshott y Allin Cottrell.
—
1 Tomas Härdin, MSc en Ciencias de la Computación, es un ingeniero investigador en la universidad de Umeå y un consultor autónomo. Sus principales áreas de interés son las matemáticas, la programación y la electrónica. Mantiene partes del proyecto de software libre multimedia FFmpeg (https://www.ffmpeg.org/ ), una herramienta de co-simulación distribuida llamada FmiGo (https://www.fmigo.net/) y partes de la radio de voz digital amateur FreeDV (https://freedv.org/ ). En años recientes, sus intereses se han desplazado hacia la cibernética. Esto incluye leer artículos y realizar experimentos sobre cosas relacionadas con la cibernética, que también están documentadas en su blog (https://www.haerdin.se/tag/cybernetics.html ).
2 Otras lecturas relacionadas:
- The People’s Republic of Walmart de Leigh Philips y Michal Rozworski
- The Cybernetic Brain de Andrew Pickering
- Brain of the Firm de Stafford Beer
Algunos nombres de este campo sin un orden particular:
Wassily Leontief, Leonid Kantorovich, Victor Glushkov, Stafford Beer, Otto Neurath.
Para los que prefieren podcasts puedo recomendar General Intellect Unit que debería estar disponible donde sea que saquéis vuestros podcasts.

![La solución del cálculo económico [1]. Cibernética, política y álgebra lineal dispersa Close up man writing code on the laptop](https://cibcom.org/wp-content/uploads/2021/12/close-up-man-writing-code-laptop-1.jpg)



