Tomas Härdin1
En este post voy a presentar dos modelos de economía que deberían ser útiles para cualquiera que quiera adentrarse en la planificación. Las economías se formulan como programas lineales y el objetivo es encontrar soluciones óptimas para esos programas. Proveeré también un esquema para un algoritmo de punto interior, mayoritariamente sacado de la literatura existente. Finalmente, diré algunas palabras sobre cómo resolver LPs (Programación Lineal) de este tipo de una manera distribuida.
Los modelos
Los modelos de economía presentados aquí utilizan algunas nociones:
- En economías reales, las empresas sólo dependen de un número finito de otras empresas mucho más pequeñas que la economía en general.
- El número medio de empresas de las que una empresa cualquiera depende está acotado por una constante q independientemente del tamaño de la economía.
- La economía tiene un conjunto pequeño de industrias esenciales y una “cola larga” mayor de industrias menos cruciales.
- Las industrias esenciales tienen muchas industrias que dependen de ellas, mientras que el resto no.
Hay tres componentes de los modelos:
- Coeficientes técnicos.
- Un número de restricciones “de cesta” extra.
- Ecuaciones de equilibrio para permitir la optimización.
La diferencia entre modelos es la estructura de las matrices de coeficientes técnicos. Cinco parámetros determinan el tamaño y densidad del sistema matricial S resultante:
- v : el número de industrias.
- q : el número de inputs que cada industria tiene, como hemos descrito antes.
- w : el número de restricciones de cesta.
- r : la densidad de cada restricción de cesta.
- o : el número de ecuaciones de equilibrio que hay que optimizar.
Los coeficientes técnicos son del mismo tipo que los usados por Leontief. Están ordenados de manera que las columnas contienen los inputs de cada empresa y las líneas corresponden a los outputs. La diagonal es la matriz identidad. Los elementos fuera de la diagonal son negativos. La matriz de coeficientes tiene que satisfacer la condición (HS) de Hawkins-Simon. Ambas matrices se han generado a través de un procedimiento de conexión preferencial, y el proceso usado es la diferencia entre los dos modelos. Más sobre esto más tarde.
Para los coeficientes técnicos, se le da al lado de la derecha una lista de demandas. La formulación de Leontief (I-A)x = d se relaja a (I-A)x >= d.
Las “cestas” son un conjunto adicional de restricciones. Permiten tener en cuenta varias tecnologías disponibles para producir un único bien, o una clase de bienes. Toman la forma Bx >= f, donde tanto B como f son no negativos. Podemos imaginar cualquier número de restricciones extra. Un ejemplo concreto sería las restricciones de nutrición del post anterior.
El nombre “cesta” viene de algo que leí sobre cómo funcionaba el Gosplan. Debido a los limitados recursos computacionales, el Gosplan no podía planear las cosas usando datos desagregados. En vez de esto, tenían que juntar grupos de bienes en lo que se llamaba “cestas” de bienes, y hacer objetivos del plan agregados. Francamente, esta es una manera bastante mala de planear las cosas y no debería pensarse que estoy a favor del sistema de planificación ad-hoc usado en la URSS. Sólo estoy usando la terminología. Hay más maneras en las que el Gosplan no fue capaz de producir planes racionales, pero esta crítica la dejo para un potencial post futuro.
El propósito de añadir restricciones extra como estas es que podamos evaluar lo que ocurre si relajamos algún conjunto de demandas (entradas en d) para liberar recursos para otras cosas. Las cestas actúan entonces como un conjunto de “checks de salud” de tal manera que no hay escaseces dramáticas de bienes esenciales. En otras palabras, d puede ser vista como un conjunto de deseos mientras que f es un conjunto de necesidades. En la ciencia económica liberal, los deseos y las necesidades se consideran demandas de importancia igual, pero el esquema presentado aquí nos da más espacio para “trastear”. Otro uso para estas restricciones es poder decir “produce al menos tantos MWh de electricidad”, sin importar particularmente cómo se produce esa electricidad. Así, uno puede chequear que pasa si las plantas energéticas de carbón van cerrándose y reemplazándose por energía nuclear y renovable.
Finalmente hay un conjunto de ecuaciones de balance sobre el cual trabaja la optimización. Este puede ser cosas como el tiempo de trabajo usado, CO2 emitido, stocks de capital consumidos. Las ecuaciones de equilibrio pueden ser dispersas, pero en estos experimentos he elegido hacerlas densas.
Para las ecuaciones de equilibrio el lado derecho es todo ceros. Es posible usar valores no nulos, pero son fácilmente sustraídos debido a la presencia de la matriz identidad. Usar ceros aumenta la dispersión del sistema y por tanto hace la solución más fácil de computar.
Finalmente, todas las variables deben ser positivas.
En resumen, el sistema se ve así:
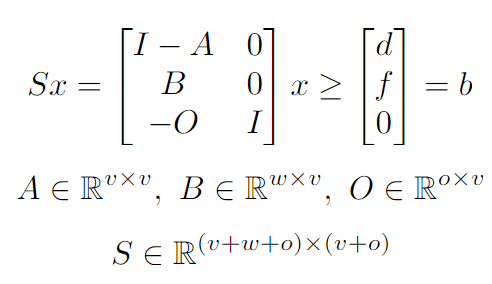
El objetivo del solucionador es encontrar la solución óptima x_* definida como sigue:
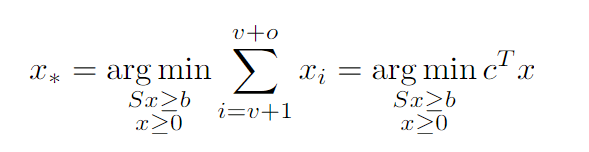
c es un vector de v ceros seguido de o unos.
La estructura descrita aquí arriba vuelve la computación de una solución inicial estrictamente factible sencilla:
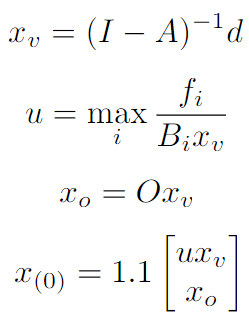
En otras palabras, primero se computa una solución de Leontieff x_v para la matriz de coeficientes. Luego, un valor u se computa para que ux_v satisfaga las restricciones de cesta. A continuación, se computa x_0 para que las ecuaciones de equilibrio se cumplan. La solución final x_(0) se crea con x_v,x_0 y u y escalada un 10% más de manera que sea una solución que esté estrictamente en el conjunto factible.
Sobre los coeficientes técnicos:
Modelo de Price
Como las industrias aparecen a lo largo del tiempo, parece razonable escoger un modelo que está diseñado para producir gráficos distribuidos como función de potencias. Un modelo así es el modelo de Price, llamado en honor a Derek J. de Solla Price. Este modelo está orientado a modelar redes de citas, que crecen con el tiempo. Los artículos (papers) más famosos tienden a ser citados más a menudo, y las citas forman un gráfico dirigido acíclico (DAG). El modelo de Price resulta en que las distribuciones de citas siguen una función de potencias.
Una desventaja del modelo de Price aplicado a las economías es que las economías del mundo real no se parecen a un DAG. El reciclaje rompe el modelo de Price especialmente. Aún con todo, este modelo es útil porque la distribución de los rangos de filas y columnas es conocida. Como la matriz de incidencia resultante es triangular, es especialmente fácil computar x_v para este modelo, requiriendo sólo O(nnz(A)) operaciones.
El patrón de dispersión del modelo de Price se ve así:
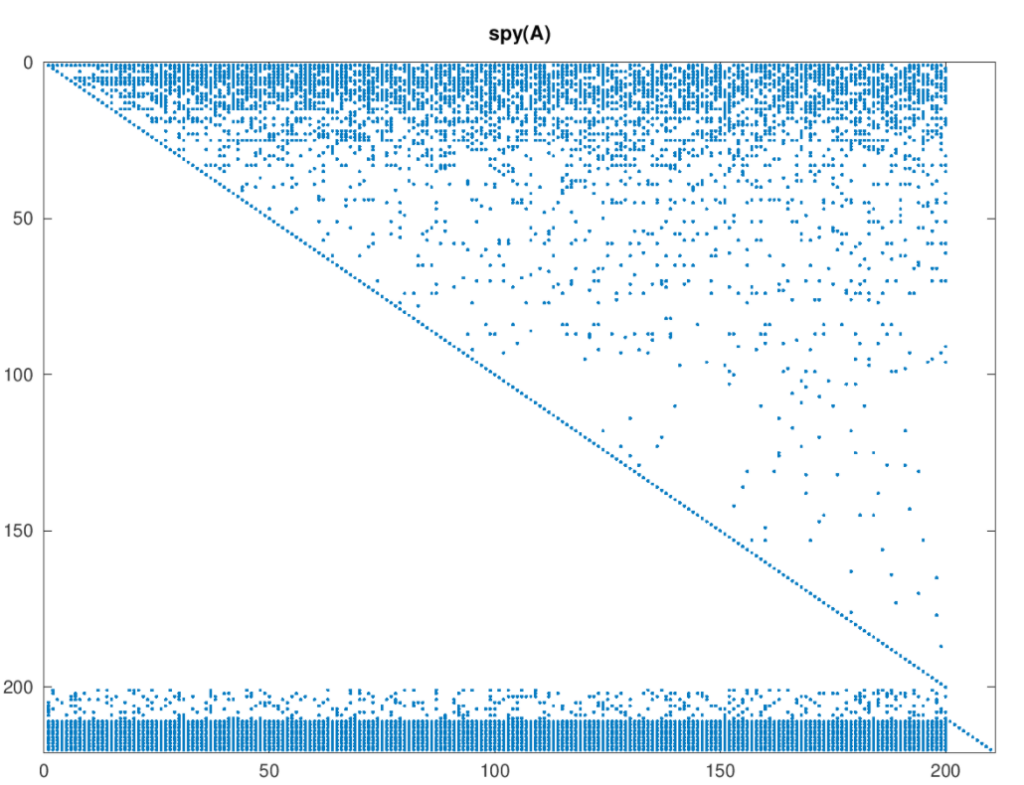
La estructura triangular es aparente, como lo son los coeficientes para las cestas y las ecuaciones de equilibrio. Para mí este, modelo parece provocar un énfasis excesivo en muy pocas industrias esenciales. También es ingenuo asumir que las viejas industrias establecidas no usan nueva tecnología. Este tampoco es el modelo con el que empecé mis experimentos.
Modelo interdependiente
El modelo inicial usado en mis experimentos es uno en el que las industrias crecen interdependientes a lo largo del tiempo. Se diferencia del de Price en el hecho de que después de cada nuevo nodo añadido, q nuevos links son equiprobables entre cualquier pareja de nodos añadidos hasta ahora. Esto produce una matriz donde los elementos no nulos están apretados en la esquina superior izquierda, siendo cada vez más dispersos hacia abajo y a la derecha:
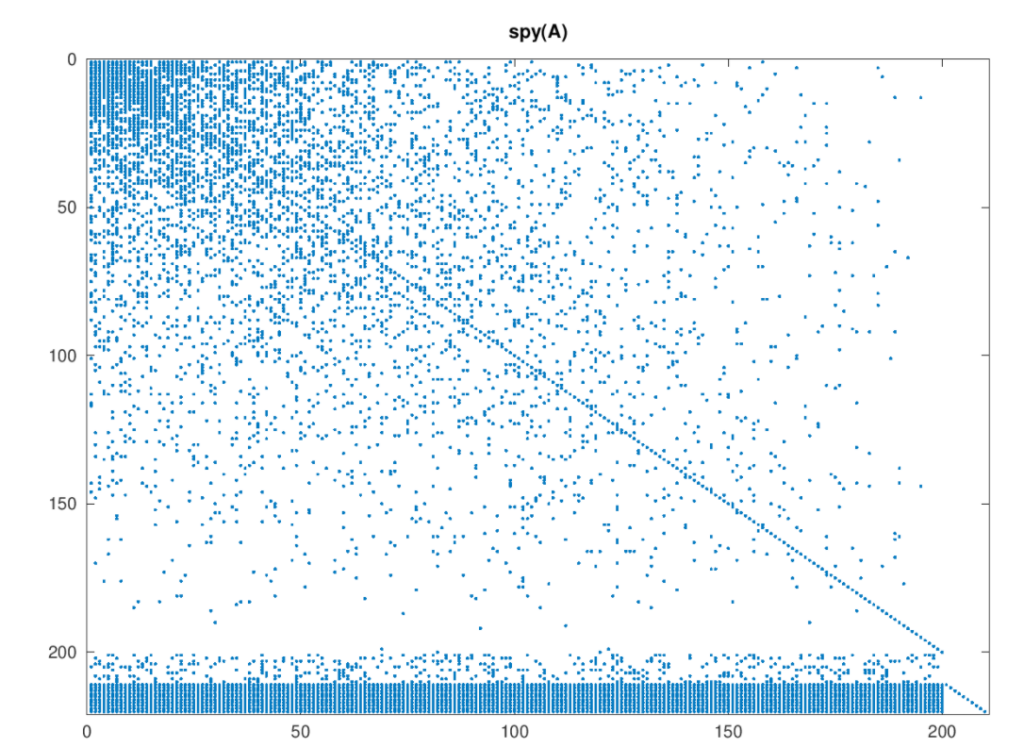
Aquí la economía es bastante explícitamente diferente a un DAG. También es más caro computar x_v, pero sigue siendo barato usando métodos iterativos. Podríamos también elegir computar la inversa del bloque superior izquierdo de las industrias esenciales explícitamente, lo cual sería útil como pre-acondicionador.
Optimalidad y la brecha de dualidad
Cuando estamos optimizando, es útil saber si estamos o no cerca de la solución óptima. Querríamos alguna información de cuánto “espacio” queda para seguir optimizando, preferiblemente un límite inferior. Si sabemos que estamos a 1% digamos de ese límite inferior, podemos parar. Estos límites inferiores son soluciones factibles dadas al dual de nuestro problema inicial (ver programación lineal dual).
En vez de buscar la solución mínima al problema primal:
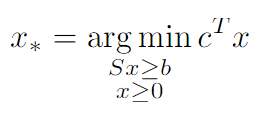
Buscamos en cambio maximizar su dual:
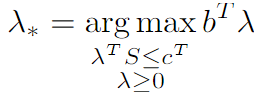
Por el teorema de fuerte dualidad sabemos que si tenemos λ_* entonces también tenemos x_* y
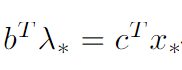
.
Todo lo que queda por hacer es computar una factible inicial λ_(0). Dejaré esto de lado por ahora.
Métodos de camino central
El solucionador que usamos está en la clase de métodos de camino central. Este tipo de solucionadores datan del artículo de James Renegar de 1988 “Un algoritmo de tiempo polinómico, basado en el método de Newton, para programación lineal”. La idea es definir una medida de “centralidad” de tal manera que un único punto es “equidistante” de todas las restricciones más la restricción c^Tx >= k_(i) definida por la función objetivo. x_(i) está cerca de ese punto central al principio de cada iteración en el algoritmo. k_(i) se actualiza entonces a k_(i+1) = δc^Tx_(i) + (1- δ)k_(i), y entonces hacemos un paso de recentrado para producir x_(i+1).
Renegar muestra que si δ=1/(13.raíz(m)) donde m es el número de filas en la matriz del sistema (m>n), entonces la distancia a x_* se reduce a la mitad a cada paso O(raíz(m)). Cada paso constituye un único paso de Newton, que toma O(mn^(w-1)) donde w es la constante de multiplicación de matrices. Consiguiendo L bits de precisión conlleva entonces O(m^1,5n^(w-1)L) operaciones.
Para el tipo de programas lineales de los que estamos hablando aquí, podemos hacerlo mejor que eso. El resultado de Renegar simplemente dice cuánto tiempo conlleva como máximo.
Métodos de predictor-corrector
Resulta que hay un límite a cuánto se curva el camino central. Esto sugiere una optimización: computar la tangente del camino central y usarla como predictor. Mover x_(i) una distancia a lo largo de la tangente, hacer un paso de corrección para acercarlo otra vez al camino central. Al mismo tiempo actualizar k_(i).
Si asumimos que el camino central no se curva demasiado, esto nos permite tomar pasos mucho más largos que δ. En mis experimentos, si se toman pasos hasta estar un 75% del camino a la restricción más cercana, en la dirección de la tangente, se consiguen 1-2 bits de precisión en vez de 1/raíz(m) con Renegar. Los siguientes gráficos representan la idea:
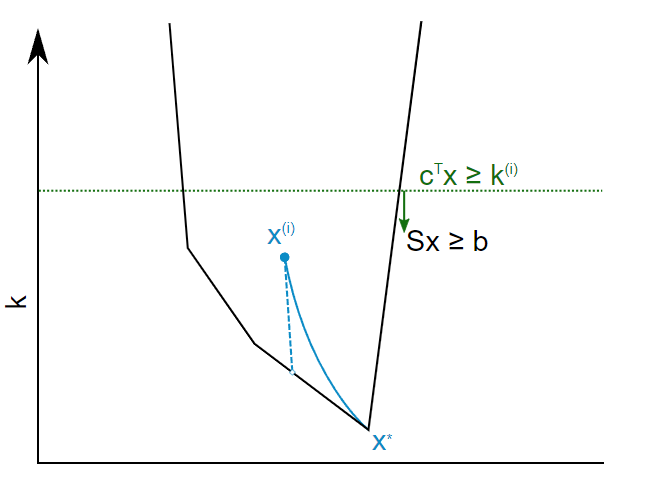
La línea punteada es la tangente al camino en x_(i). Esto puede ser computado numérica o analíticamente. El algoritmo presente lo hace numéricamente.
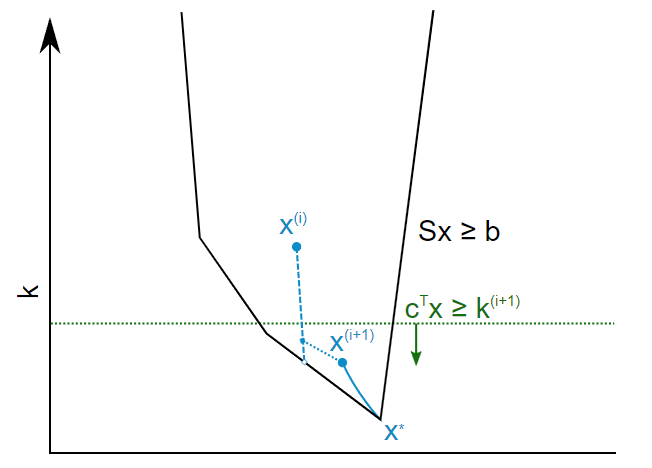
Se toma un paso intermedio a lo largo de la tangente, luego se computa k_(i+1). Entonces actualizo k de tal manera que la distancia es la mitad de la siguiente restricción del sistema. Finalmente, el punto intermedio se recentra, produciendo x_(i+1).
La desventaja de este método es que el recentrado requiere más trabajo. Curiosamente, nunca toma más que unos pocos pasos de Newton, ciertamente muchos menos que raíz(m). El trabajo requerido para el recentrado también es muy paralelizable. En realidad, es resolver h en el siguiente sistema:
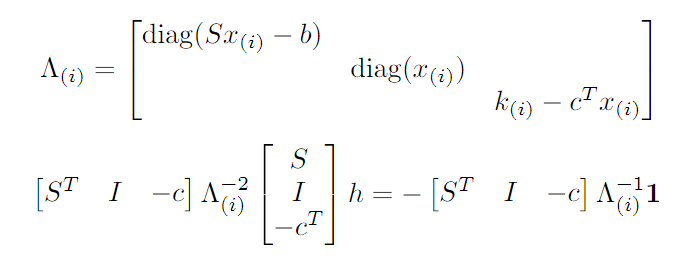
1 es un vector de unos. La matriz del lado izquierdo en la segunda ecuación es simétrica y definida positiva. Esto significa que podemos usar el método de gradiente conjugado (CG). Para CG, la matriz del lado izquierdo no necesita ser formada explícitamente. Por tanto, cada iteración sólo necesita hacer un trabajo O(nnz(S).
Para el problema dual se hace un proceso similar, excepto que todas las matrices están traspuestas, algunos signos cambian y c y b intercambian roles.
Resultados
Los tests se hicieron en un HP Compaq 8200 Elite SFF PC (XL510AV) con un i7-2600 @ 3.40GHz y 8 GiB 1333 MHz DDR3 ejecutando Debian GNU/Linux 10 (buster). Esta implementación está escrita en GNU Octave, que paraleliza algunas de las computaciones, pero para nada todas.
Se hace pasar v por los valores 300, 1000, 3000, 10000, 30000, 100000, 300000. Los otros parámetros son q = 160, w = 10, r = 160 y o = 10. El wall time (tiempo de ejecución del programa), número de iteraciones CG y la brecha de dualidad final se miden para cada ejecución. Se hacen ejecuciones para los dos modelos. Las condiciones para parar son una de las dos:
- La brecha de dualidad es menos que 1%
- En la última iteración se hizo una mejora de menos de 1 ppm
La segunda condición es necesaria por culpa de un bug en el código que no he identificado todavía. Una ejecución incluso falló a la hora de encontrar una solución decente, v = 100000 para el modelo Price. Omití esa ejecución en los resultados. De manera similar v = 1000000 también falla, pero para ambos modelos, lo cual explica que 300000 sea el último punto.
El siguiente gráfico enseña los wall times de cada ejecución en función del nnz(S) y muestra una función de potencia ajustada a los resultados:
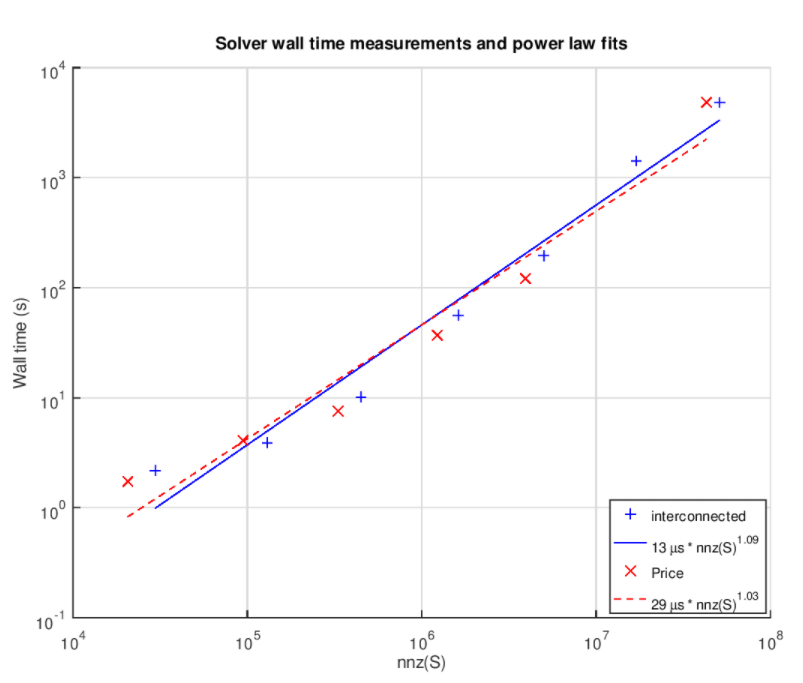
El ajuste casi lineal es muy prometedor. Hay que tener en cuenta que esto es para esta clase específica de problemas, y es casi seguro que no se aplica en general a resolver PLs.
Algunas ejecuciones no consiguen llegar debajo de la marca de 1%:
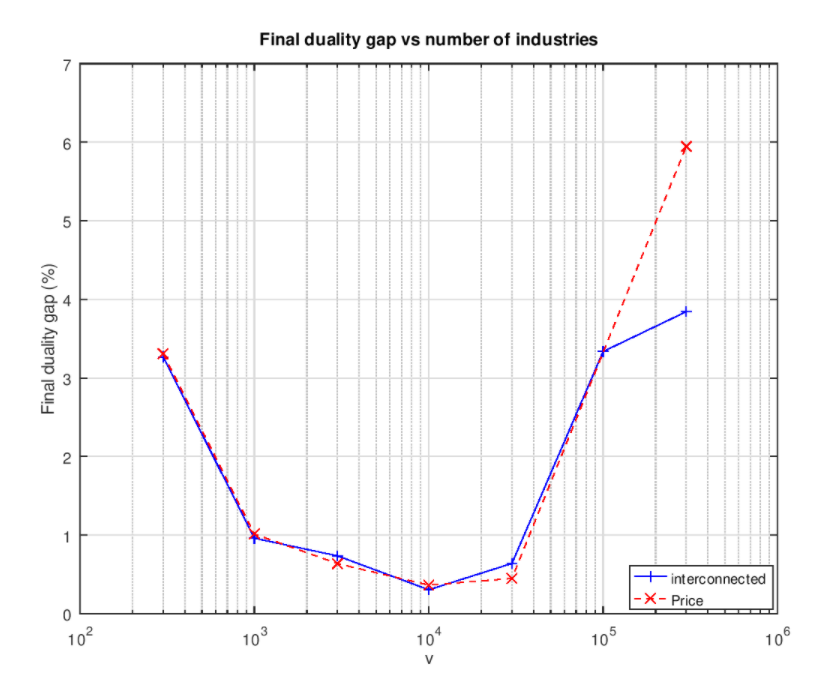
Esto sugiere que hay más trabajo que hacer. Sale un gráfico de forma similar cuando trazamos el número total de pasos del gradiente conjugado vs el número de industrias:
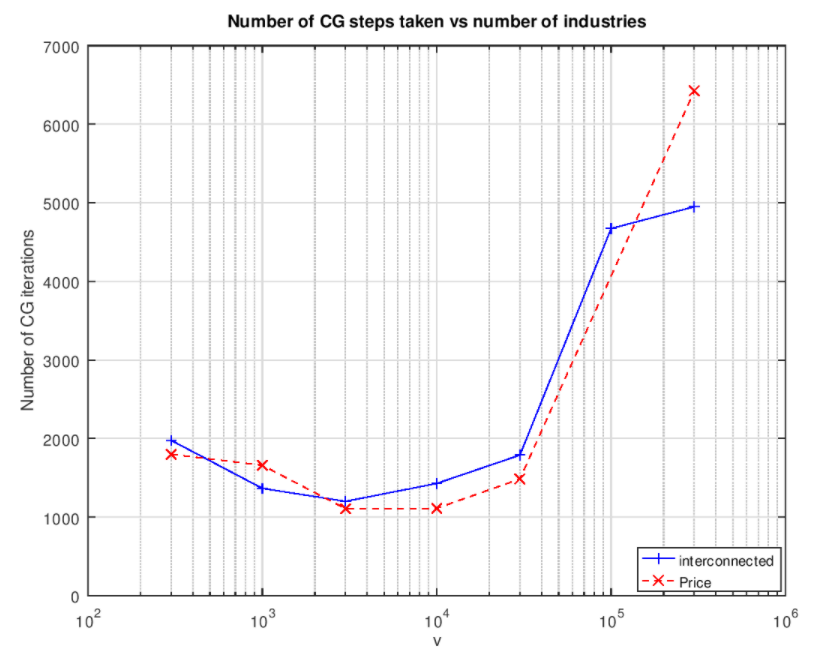
Curiosamente, el número de pasos es de entre 1000 y 2000 en el caso de las ejecuciones que encuentran una solución de 1%.
Paralelismo
La operación central del algoritmo de Renegar y de sus descendientes es el paso de centrado de Newton. Los trabajos recientes en este campo se han centrado en acelerarlo al mantener una aproximación de la inversa de la matriz del lado izquierdo. Por ejemplo, el trabajo de Lee y Sidford. Estos esfuerzos son en serie y no tan útiles para lidiar con sistemas lo suficientemente grandes.
Otra manera de lidiar con esto es paralelizar el solucionador de Newton. Si dejamos escalar al número de nodos con el número de no nulos de S entonces el tiempo para cada paso se convierte en constante, más algo de comunicación por encima. Si usamos el resultado más conservador de Renegar para el número de pasos, entonces el tiempo total para resolver la PL es O(raíz(m)L). Gracias al experimento aquí presentado sabemos que un solo ordenador con 8 GiB de RAM puede lidiar con un programa lineal correspondiente a una economía con un millón de industrias. No parece, por tanto, poco razonable que la totalidad de la economía mundial, un sistema con miles de millones de industrias, pudiera planificarse usando un grupo de ordenadores relativamente modesto.
1 Tomas Härdin, MSc en Ciencias de la Computación, es un ingeniero investigador en la universidad de Umeå y un consultor autónomo. Sus principales áreas de interés son las matemáticas, la programación y la electrónica. Mantiene partes del proyecto de software libre multimedia FFmpeg (https://www.ffmpeg.org/ ), una herramienta de co-simulación distribuida llamada FmiGo (https://www.fmigo.net/) y partes de la radio de voz digital amateur FreeDV (https://freedv.org/ ). En años recientes, sus intereses se han desplazado hacia la cibernética. Esto incluye leer artículos y realizar experimentos sobre cosas relacionadas con la cibernética, que también están documentadas en su blog (https://www.haerdin.se/tag/cybernetics.html ).

![La solución del cálculo económico [3]. Complejidad de planificación para economías modelo](https://cibcom.org/wp-content/uploads/2022/01/man-calculating-writing-close-up-1.jpg)



