Tomas Härdin1
En el post anterior expuse un esquema a favor de la planificación por ordenadores. En este post presentaré algunos ejemplos que deberían ayudar a transmitir la idea general.
Una pequeña economía de ejemplo
En estos ejemplos voy a usar una economía que sólo produce un bien. Este bien puede ser lo que sea, por ejemplo, comida. Hay dos tecnologías disponibles para producir este bien: techA y techB. La diferencia entre las dos tecnologías es que techA usa 2 unidades de trabajo y 3 unidades de emisiones de CO2 por unidad de producción mientras que techB es el opuesto: 3 unidades de trabajo y 2 unidades de CO2. Se complementan cada una y la elección entre ellas depende de si queremos minimizar la cantidad de trabajo requerido, la cantidad de CO2 emitido o alguna combinación de ambas. Dada una demanda d, un trabajo máximo L_max (labour en inglés) y unas emisiones máximas de CO2 C_max, tenemos la siguiente ecuación matricial:
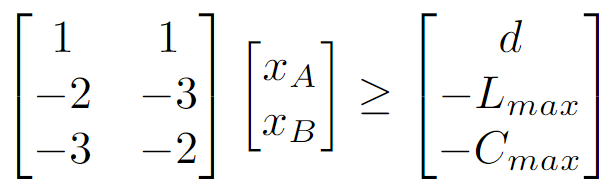
Tanto x_A como x_B son no negativas, lo que significa que x>0. Todas las x’s se asumen no negativas en el resto del artículo.
Aislada, la anterior ecuación no es muy útil ya que ni el trabajo ni el CO2 son variables. Para poder optimizar alguna de estas, necesitamos extender el sistema. Empecemos minimizando el trabajo, lo que requiere añadir una tercera variable x_L:
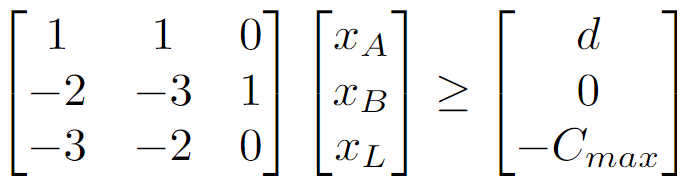
La nueva columna en la matriz convierte la segunda línea en una “ecuación de equilibrio”. Al estar minimizando x_L, el objetivo es añadir lo menos posible manteniendo la suma de trabajo añadido y trabajo consumido no negativa.
La solución óptima x_* que buscamos viene dada por:
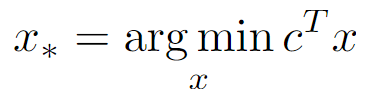
Donde:
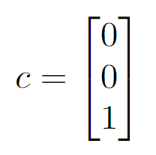
La solución depende sólo de d y C_max. Si dejamos C_max=5 entonces podemos barrer d desde 0 hasta 2,5. El siguiente script de bash hace esto mismo, usa lp_solve para solucionar el programa lineal resultante, analiza el resultado y devuelve código Octave que renderiza el gráfico de abajo.
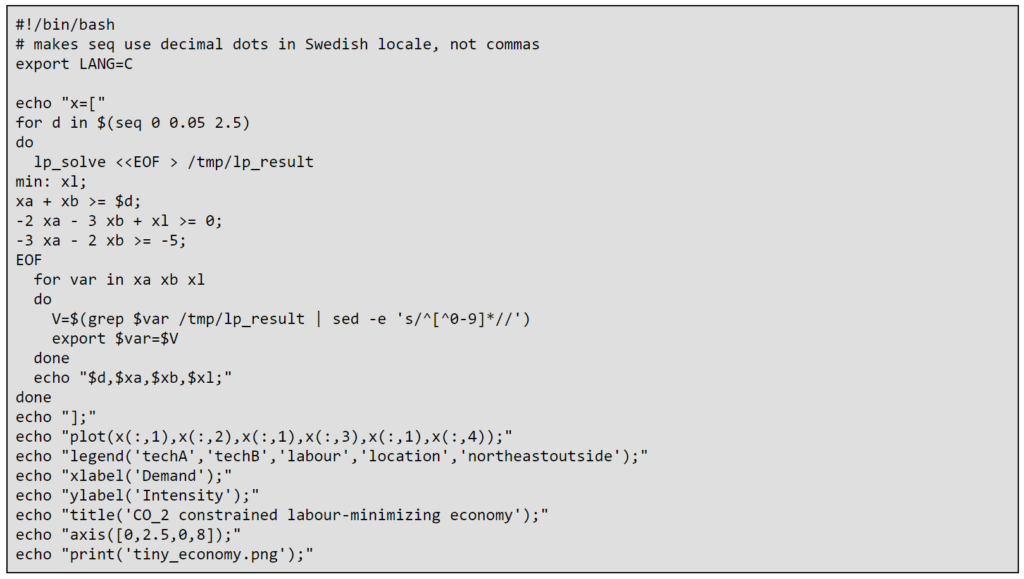
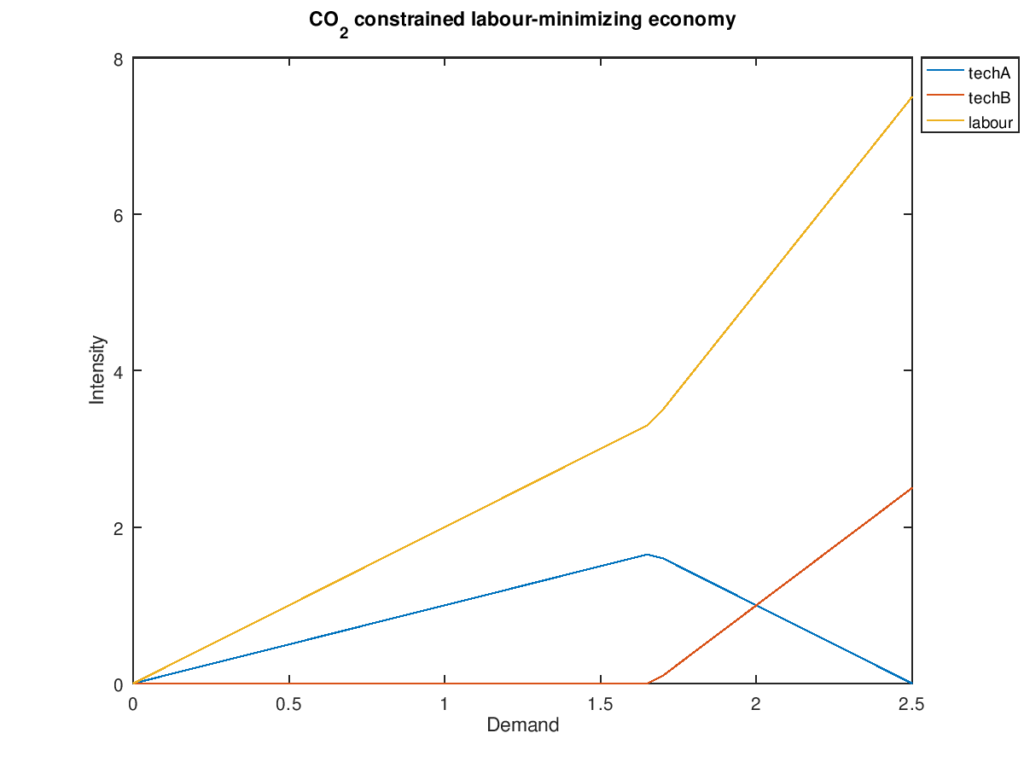
Podemos ver que techA es preferida mientras las emisiones de CO2 estén bajo el límite. Una vez que la demanda va más allá de 1,66 techB empieza a ser usada y la demanda marginal de trabajo aumenta.
Si, en cambio, minimizamos emisiones CO2 entonces el resultado parece muy parecido excepto que techA y techB intercambian roles:
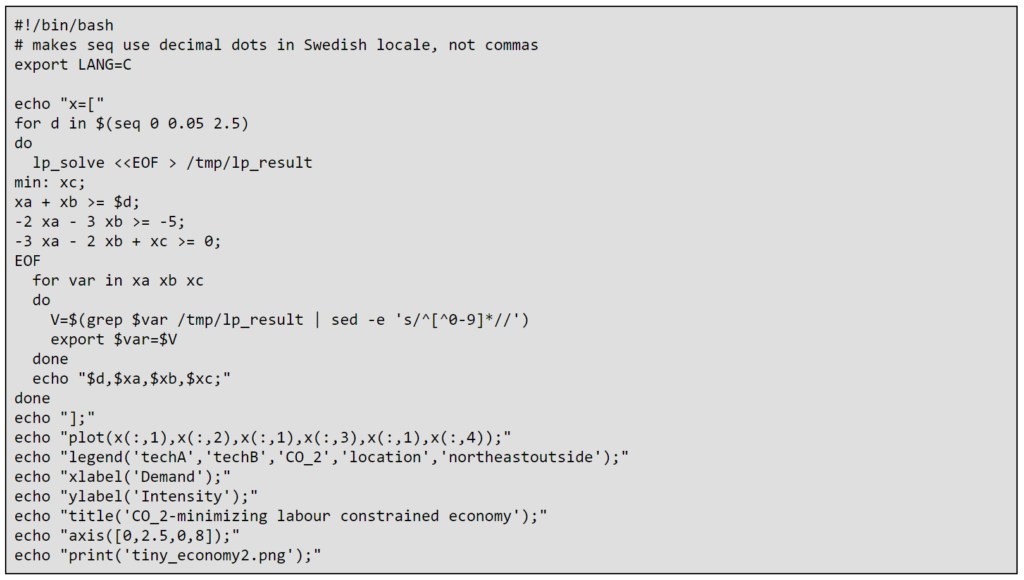
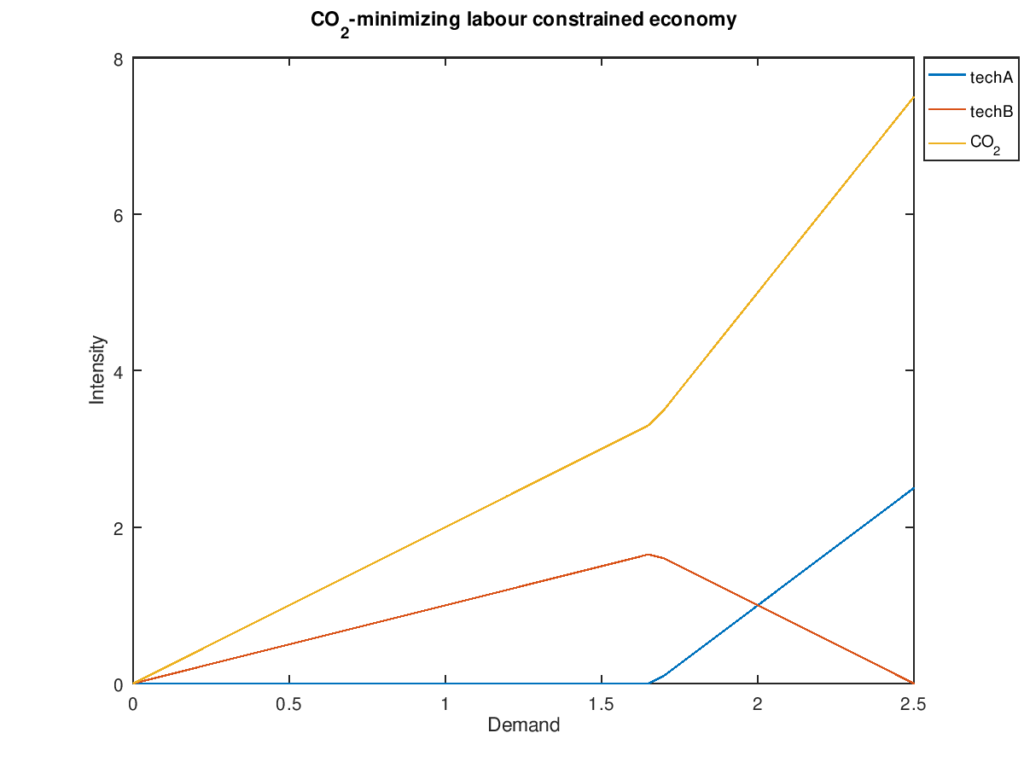
En realidad, podemos querer minimizar una combinación de trabajo y CO2. El siguiente es un ejemplo interesante:
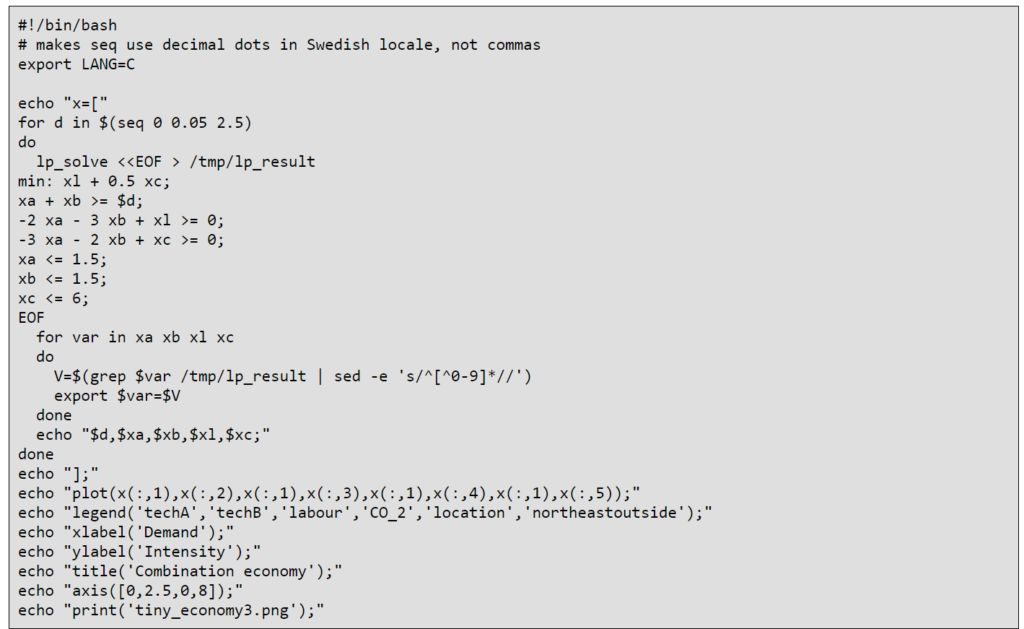
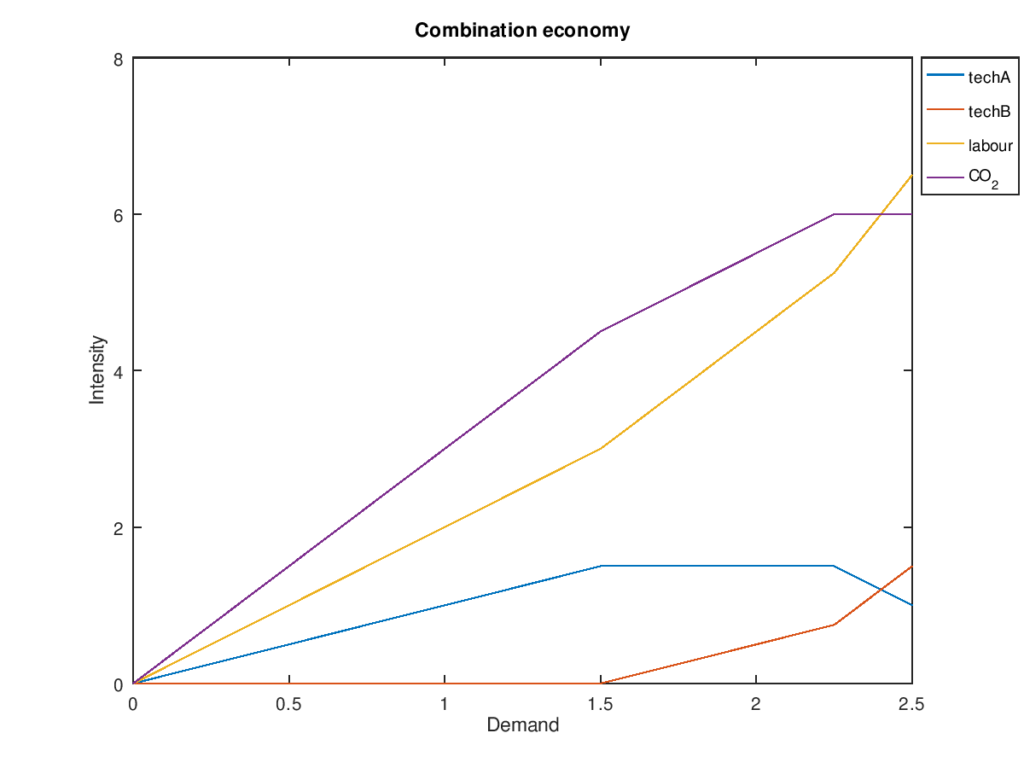
En este ejemplo las capacidades de techA y techB son limitadas. Cada una puede producir 1,5 unidades del bien. Además, las emisiones de CO2 están limitadas a 6 y tratamos de optimizar una mezcla que favorece el trabajo. Tres regiones diferentes son claramente visibles. La primera región no está acotada, la segunda lo está por las capacidades de techA y la tercera está acotada por el CO2. Según la “demanda”/presupuesto marginal de CO2 decrece, la demanda marginal de trabajo aumenta.
Las ecuaciones para este sistema son así:
Aquí he elegido hacer condiciones de no-negatividad en x explícitas, para resaltar que la matriz entera es alta. Podemos también ver que el sistema es bastante disperso y que puede ser ligeramente simplificado:
Otros ejemplos
Economía en cadena
Una economía en cadena tal que A->B->C->…Z donde cada industria necesita dos unidades de la industria anterior, una unidad de trabajo y una de CO2, se ve así:
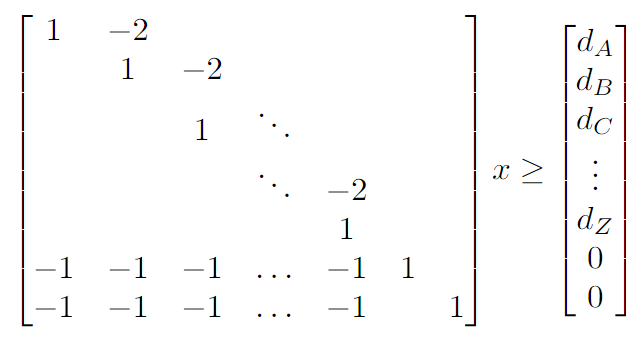
Economía de servicios
Los servicios son industrias que nominalmente sólo requieren trabajo. En la práctica, requieren más que eso, como suministros de oficina. Los trabajadores de servicios también tienen que comer, pero eso se trata en otro lado en las ecuaciones. Las industrias de servicios no emiten CO2 por sí mismas pero pueden hacerlo indirectamente como todas las industrias hoy en día:
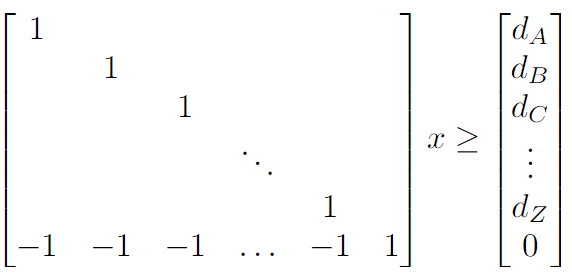
Producción de comida
Para asegurarse de que todo el mundo tiene comida y que hay variedad, uno añade un número de condiciones. La más importante de esas son las que se refieren a los macronutrientes como la energía, los carbohidratos, la grasa, la proteína etc… Si fuéramos a depender únicamente de los nutrientes entonces la solución acabaría eligiendo probablemente un único tipo de cultivo como maíz o sorgo. Aunque esto mantenga a la gente alimentada, sería una dieta muy deprimente.
Podemos usar estadísticas de qué tipos de comida la gente prefiere y añadir una condición para cada una: producir al menos d_Po de patatas (potatoes), d_CM de leche de coco (coconut milk), d_Ha de habaneros etc… También es verdad que las preferencias varían según la estación y las regiones. Sabemos con mucha certeza que la demanda de torrijas va a ser alta en semana santa pero baja comparativamente el resto del año.
La demanda de ciertos bienes varía con una frecuencia diferente de la del año gregoriano. Por ejemplo, los bienes asociados con el Ramadán y tradiciones similares siguen el calendario lunar. Para comidas regionales, diásporas considerables tienen que ser tenidas en cuenta.
Para los diez alimentos básicos listados en Wikipedia1, el programa lineal para cuánta área de cada cultivo puede ser construida es:
Cada columna corresponde a un cultivo básico desde maíz a plátano y la columna final es para minimizar el área. Los valores están pesados por cuánto se produce por hectárea (en el país más productivo al respecto) para cada cultivo. Las filas están escaladas de manera que los valores de la novena columna (sorgo) sean todos uno. El lado derecho está dado por la columna RDA en el artículo de Wikipedia y representa cuantas hectáreas tienen que ser cultivadas para producir 10,000 días/persona de comida para cada nutriente.
Las filas corresponden a la energía, proteínas, carbohidratos, fibra, ácidos grasos monoinsaturados y ácidos grasos poliinsaturados. La fila final es la ecuación de equilibrio para el área.
Podemos ver de un vistazo que el sorgo es el cultivo más eficiente en términos de área, con 0,26 hectáreas siendo suficientes para suplir 10,000 días/persona de macronutrientes. El factor limitante son los ácidos grasos monoinsaturados. Si el aceite de canola se usa para la grasa, entonces el área necesaria se reduca a en torno a 0,11 hectáreas.
Este tipo de dieta en realidad solo sería aceptable en circunstancias extremas. Como dije en el comienzo de esta sección, uno añadiría condiciones extra para que algunos cultivos sean cultivados porque la gente lo quiere. Los resultados también varían dependiendo de la localidad, pero añadir variables extra por localización en la cuadrícula para su optimización no entraría en un post de blog.
1 Tomas Härdin, MSc en Ciencias de la Computación, es un ingeniero investigador en la universidad de Umeå y un consultor autónomo. Sus principales áreas de interés son las matemáticas, la programación y la electrónica. Mantiene partes del proyecto de software libre multimedia FFmpeg (https://www.ffmpeg.org/ ), una herramienta de co-simulación distribuida llamada FmiGo (https://www.fmigo.net/) y partes de la radio de voz digital amateur FreeDV (https://freedv.org/ ). En años recientes, sus intereses se han desplazado hacia la cibernética. Esto incluye leer artículos y realizar experimentos sobre cosas relacionadas con la cibernética, que también están documentadas en su blog (https://www.haerdin.se/tag/cybernetics.html ).
