Lex Kravetsky
Lex Kravetsky is a programmer and mathematician who posts ample content on different topics on his YouTube channel (https://www.youtube.com/@KravetskiLex) and on different blogs (https://lex-kravetski.livejournal. com). The original version of the article in Russian can be found at: https://22century.ru/popular-science-publications/direct-democracy-1
The article is the first part of a series of three.
Can direct democracy (or «quasi-direct» in the case of ad hoc proxy voting) be more effective than representative democracy? Let’s try to find out.
What is «direct democracy»?
Direct democracy is sometimes understood as direct voting for the executive or any other power, as opposed to a system in which power is elected by a legislature, which, in turn, is already elected by the citizens (this system, in particular, operates in the USA during presidential elections).
However, a more frequent and, in my opinion, currently more correct interpretation of the term is: a system in which all or most decisions are taken directly by general vote. This system is used for various issues, for example in Switzerland in the form of referendums and also in some public organizations.
On the «waste of time» of direct democracy
Often, critics of direct democracy will ask the question, «How will everyone manage to find the time to resolve and vote on each issue?»
The answer is: of course they will not.
One proposal to solve this problem, proxy voting, suggests direct democracy must be accompanied by a mechanism of proxy voting, in which each person can appoint any number of “delegates” and, in cases where that person does not vote, their vote will instead be distributed equally among their voting delegates.
Delegate selection can be greatly simplified by eliminating the overlaps between each person and each potential delegate candidates, determined where both voted in person
The candidates themselves, should also be members of the same group to which the question belongs (all residents of the house, city, country, social organization, etc.).
A deeper dive into this proposition is a topic for another article, and we will deal with other issues here.
Intuitive errors
Before the development of the Internet, direct democracy was not easy to organize, because, as was done in, for example, the ancient Greek city-states, all participants had to gather simultaneously in the same place, and votes were counted approximately, not precisely. Today, however, the existence of the Internet makes such technical errors non-issues. Instead, these difficulties are mainly psychological.
Even among supporters of direct democracy, one often hears statements like “Of course, direct democracy works more slowly and errs more often due to the voters’ lack of professionalism than a system with a leader at the head, but with it, decision-makers are less likely to be volunteers, it is fairer, more reflective of the majority view, and usurpation of power is very difficult.”
“It works slower” is a statement that seems counterintuitive, but probability theory is very often counterintuitive, and as a result what seems intuitive can be far removed from reality.
This question is a case in point.This article intends to show that the first part of that statement is not actually an actual drawback of direct democracy. Without detracting from the intuitive reasoning towards the benefits of direct democracy, this is because the first part of the statement – the enumeration of the drawbacks of direct democracy – is in fact based on pure speculative judgments, which don’t actually hold true to reality. This article will no longer remain within speculative demonstration, but instead will be based on probability theory and experimental evidence from statistical models.
Terminology and «rules of the game
There are many variants of direct democracy, with their many differences and many similarities (the common thread being that all citizens, and not a small group, decide on every issue). However, these differences fundamentally affect both the analysis and the conclusions to be drawn from it. Therefore, a variant of direct democracy, consistent with the following principles, will be considered:
1. One person, one vote.
2. The decision is made by majority vote.
In addition:
1. For simplicity, it is assumed that for each question the choice is between two answers.
2. Also, for simplicity, it is assumed that all participants have voted in full (except in sections where speed of decision making is investigated).
These two clauses do not significantly affect the conclusions, but they make it much easier to understand the patterns inherent in direct democracy.
There are a few more terms that will need to be defined:
“Participants” are all those who make decisions with their votes. Their synonym is the word “voters”. And as a whole, the voting body of participants will be referred to as the “collective”.
In contrast to this system, a system in which one person makes the decision will be considered. Regardless of whether it is a monarch, an elected president, or an informal leader, this article will refer to them as a “dictator” and the system “dictatorship”.
While it may seem that such a person should be called a “leader” instead of a “dictator”, the word “leader” has too many meanings to be precise. It can be, for example, a respected person or a person who inspires people to do something. However, in the context of the problem at hand, only one feature of the “leader” is important: the right to make decisions in a monopolistic way, i.e. to “dictate” decisions to everyone else. Therefore, the term “dictator” is more associated with this right than “leader”, and that is why it is used. This term should not at all be understood as an attempt to denigrate an abstract “leader” with a term that has negative connotations.
Moreover, this article shows that the issues considered by the voters rather than a dictator have an objectively better solution.
It is a simple fact that many of the questions that a collective or a dictator may face do not have a “right” answer. For example, the color that should be painted on the walls of the entrance hall depends exclusively on the preferences of the majority of the residents of that hall. And here green is no more “objectively correct” than blue: it all depends on which one the average tenant likes better. Even a consideration along the lines of “such-and-such color is relaxing” will not help in this case, because while that may be the case, there might be a majority of people living in the building who find the color irritating, or simply may not want the walls to be relaxing.
On the other hand, the choice between, for example, spacecraft projects to colonize Mars can already be made right or wrong: choosing an objectively better (in the sense of achieving that set goal) or worse project. This is fundamentally different from a “declaration of intent”: the decision that the majority of, say, a country’s citizens would like to colonize Mars in the near future, so they set such a goal and are willing to spend part of the country’s available resources on it.
It hardly makes sense to argue that direct democracy will choose the right option among questions about “tastes” or “objectives”: after all, each person is more or less aware of what colors – or whatever else the question deals with – they like. This is why, when the mythical disadvantages of direct democracy are discussed, it will not be about such questions, but instead only about those in which there is an objective answer to the best of two options, which can be experimentally checked. Using logic, if multiple choices are given, one can be objectively wrong. Precisely this type of question is implicit in the following text.
The simplest decision-making model
Let us assume that:
There is a collective of a given number of people, each of whom can choose one response option from two available choices.
The option that obtains the most votes wins.
If a tie occurs (which is only possible with an even number of participants), we will assume that the team has chosen the wrong option.
Each vote assumes that there is one correct and one incorrect answer. Each participant has the same probability of choosing the correct one.
How exactly each participant analyzes the question is omitted: in fact, the probability of making the correct decision only emulates the result of all these mental fluctuations, reasoning, conjectures, etc., that lead each participant to the correct or incorrect answer.Essentially, this means that in a specific percentage of cases each participant makes the right decision and in all other cases he/she is wrong (which could be statistically proven, perhaps by the results of many previous polls after the consequences of this or that decision became known). Therefore, in this model, it assumes that each voter has the same chance of choosing the right decision.
Probability of a correct collective decision
The probability of obtaining a correct decision by direct voting is deduced from the following considerations.
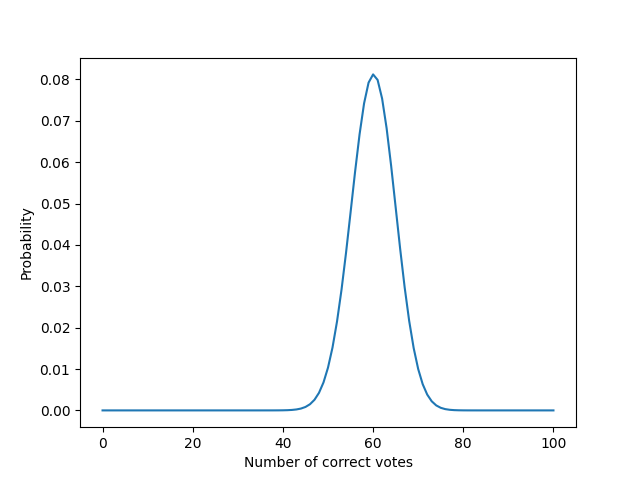
The voting results have a binomial distribution, so the function describing the probability of obtaining the number of affirmative votes equal to ‘x’ in this distribution is the following.
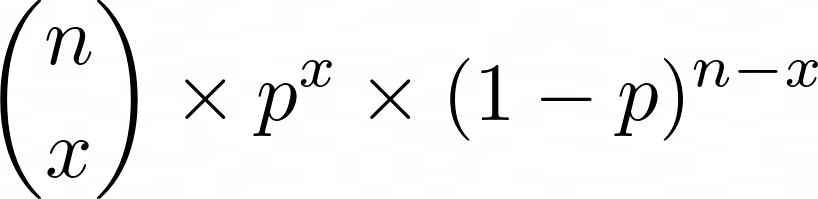
Here ‘n’ is the number of voters, and ‘p’ is the probability that each voter makes a correct decision.
What appears in parentheses is the «binomial coefficient».
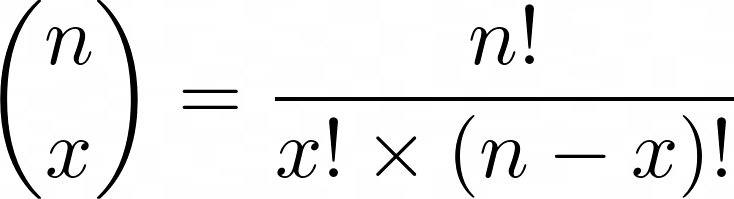
The exclamation point represents the factorial function, which outputs the product of all numbers from 1 to n:

An example of binomial distribution for 100 voters and a probability of choosing the correct answer equal to 0.6 for each participant.
The option with the most votes wins, so to find the probability that the correct option wins we have to add up (or integrate) all those options in which the correct option has received a certain number of votes, more than half of the participants.
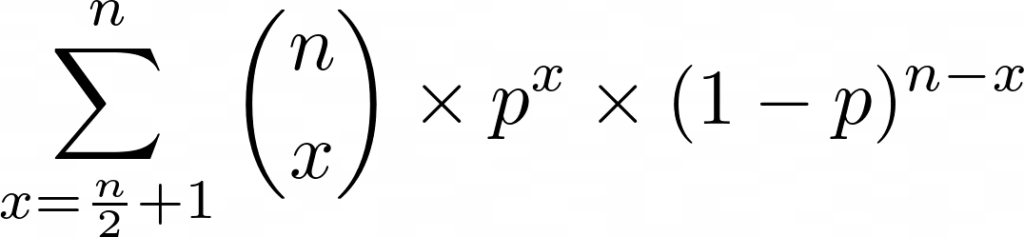
In order not to confuse the letters later, let the number of participants be called ‘nall‘, and let the probability of a participant making a correct decision be p1.
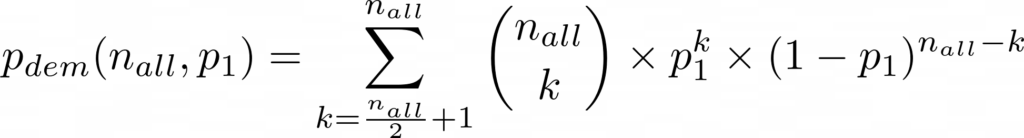
Comparing the results of this formula with the results of the random number simulation (which simulates only the selection process with a given probability of each participant), we can see that this function (green in the graph) indeed correctly shows this pattern (the X axis shows the probability of each participant guessing correctly, and the Y axis shows the probability of the whole collective guessing correctly according to the results of the voting).
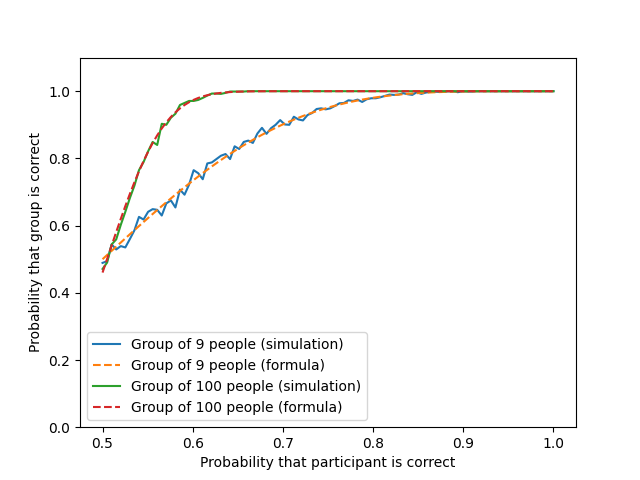
Unequal odds for participants
The question arises as to whether it is correct to model this process with the same probability of success for each participant.
After all, it is true that people may have different knowledge of the subject and different intellectual abilities, and therefore, in each case and even in general, some people will get the correct solution more often than others.
However, when dealing with a large sample, people’s abilities tend to have a Gaussian distribution. Therefore, their probability of choosing the right decision as a function of their skill and knowledge is likely to have a Gaussian distribution as well.
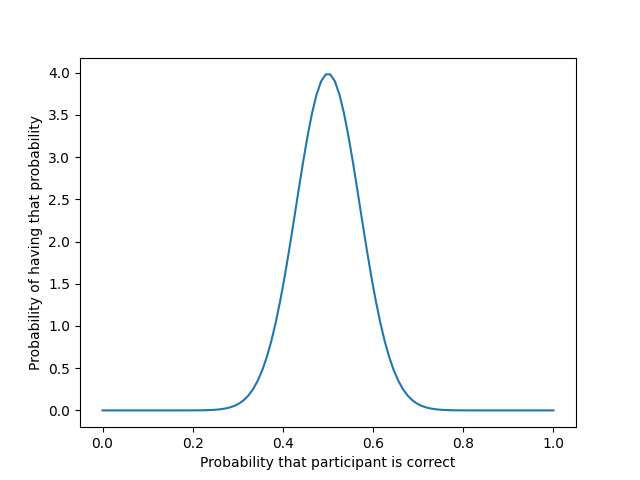
If we simulate a process that takes into account a Gaussian distribution of hit probabilities among voters (such as this one), you get more or less the following image.
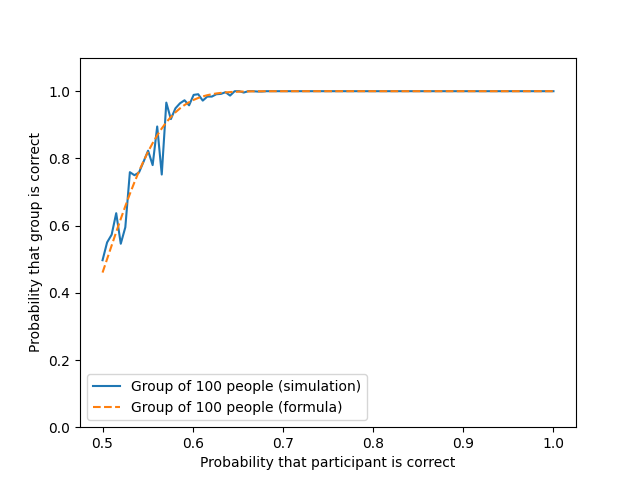
The graphs, as can be seen, coincide with the accuracy of small uniform fluctuations in both directions, i.e., the results of such models are identical.
That is, with a normal distribution of hit probabilities and a relatively large number of participants, the results are mainly affected by the average hit probability of the whole group, so it can be simply attributed to each group member, which will not noticeably affect the adequacy of the model.
Case Study
Now that we have a formula to express the probability that the collective makes the correct decision and have shown its accuracy, let us see how this probability behaves as a function of the number of voters and the probability that each voter makes the correct decision. The outcome may be surprising.
For example, if the probability that each member of a collective of 1000 makes a correct decision is 0.51 (makes a correct decision 51% of the time and an incorrect decision 49% of the time), then the entire collective would appear to make the correct decision approximately 73% of the time by majority.
Yes, only a two percent margin of probability of making the right decision over the wrong one in a vote of 1,000 people is enough for the collective to make the right decision by majority 73% of the time.
In other words, a dictator would have to get it right with a probability of 0.73 (compared to 0.51 for each member of the collective) to match his decision-making efficiency with that of the collective.
This difference in probability may not seem very significant: the dictator is a professional and, therefore, can get it right more often than all these non-professionals, but consider the following: in this case, each participant gets the right decision only slightly better than a coin, but in order to be comparable to the collective, the dictator should already have to get it right 50% of the time more than the average voter. While this is very possible, the guessing probability of each voter may be higher as well.If we plot the probability of the collective being right from the probability of its members being right, it will look like this (as before, the X-axis shows the probability of each member being right, and the Y-axis shows the probability of the collective being right by the voting results):
It can be seen from the graph that when the probability of each participant making a correct decision reaches approximately 0.56, the probability of the whole group making a correct decision is already so close to 100% that it cannot be seen in the graph.
If we were to simulate this numerically with random numbers, it would take billions of attempts for the wrong decision to occur at least once, with each voter having even a 60% probability of making the correct decision. In this case, the probability of a correct collective decision is 0.9999999999999999. Is it possible to find such a “professional dictator” in reality? One that can be considered to never be wrong at all?
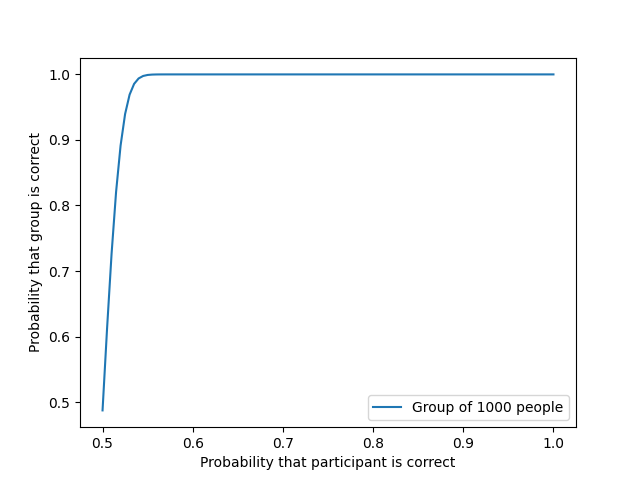
If we take a larger team of 10,000 people, the slope at the beginning of the curve becomes almost vertical: it approaches 100% very quickly:
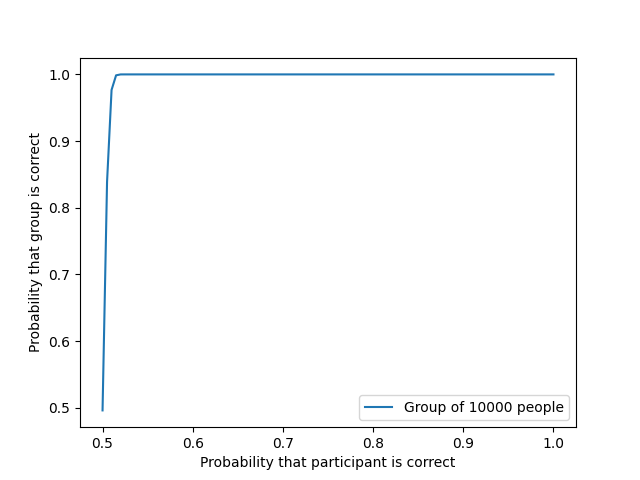
For a collective of this type to make a mistake only once in a hundred, its members only need to make the correct decision with a probability of 0.512, or 51.2% of the time.
On the other hand, if we take a smaller collective of 100 people, the interval in which it is possible for a dictator to be able to compete with the collective in terms of probability of making correct decisions increases:
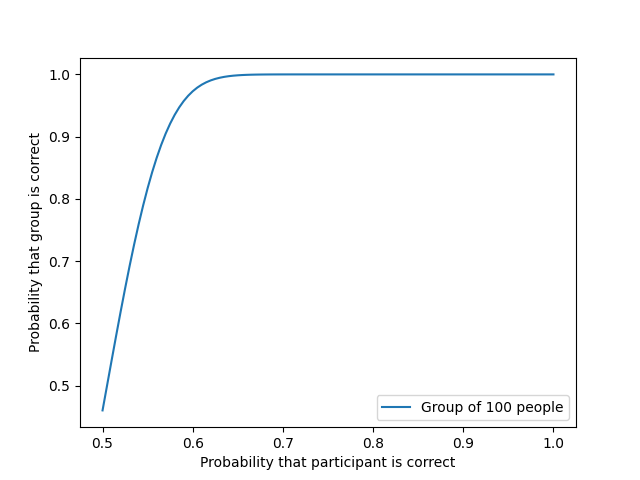
The effectiveness of direct democracy as opposed to representative democracy
The conclusion to be drawn from the above is quite counterintuitive.
In philosophical debates on direct democracy one often hears something like: “Well, yes, when we have a few people – a council of a dozen specialists, for example – democracy still works, but with hundreds of thousands of people the probability of making the right decision is very low.” This – even philosophy at first glance – is justified by the fact that “hundreds of thousands of people are mostly laymen, so of course, many of them will be wrong and the decision made by the majority will be wrong, while a smart and professional dictator will probably guess better”.
However, the above analysis shows the opposite: the larger the collective, the better the dictator’s guessing (with the same average probability of guessing of the participants) must be in order to surpass this collective in decision making. Moreover, for a sufficiently large collective (more than ten thousand people), there can hardly exist in reality a dictator comparable to this collective in guessing quality, even if the guessing probability of each participant is minimally higher than the choice by coin toss.
Consequently, the larger the team, the lower the average hit probability of the participants needed to find a particular dictator.
Here are some example values (unit probability here means that a point is followed by at least twenty nines).
| Number of participants | Probability of a participant making the correct decision | Probability of the group making the correct decision |
| 100 | 0.51 | 0.54006575973257371636 |
| 100 | 0.6 | 0.97290080224299099495 |
| 100 | 0.7 | 0.99997793908667283401 |
| 1000 | 0.51 | 0.72609855573050397656 |
| 1000 | 0.6 | 0.99999999989851969616 |
| 10 000 | 0.51 | 0.97671828748073061717 |
| 10 000 | 0.6 | 1.0 |
| 100 000 | 0.501 | 0.73542218160338154516 |
| 100 000 | 0.51 | 0.99999999987093485613 |
The right column shows the probability with which the dictator must be right to be as good as the collective with the relevant parameters.
It is easy to see that even with quite small numbers and quite low guessing accuracy of the collective members, the dictator would need to have a completely unrealistic guessing probability, in practice indistinguishable from “never wrong”, in order to remain competitive.